Aktivační funkce: skoková, lineární, sigmoidní, ReLU a Tanh

Dnes se podíváme na aktivační funkci: jak ji vybrat a jaké jsou výhody a nevýhody různých typů aktivačních funkcí – od krokové až po hyperbolický tangens.

Materiál je rozsáhlý, proto doporučujeme si jej pro budoucí použití uložit do záložek.

OBSAH

Obecné informace: jak fungují neurony

Aktivační funkce:

1. Prahová (skoková) funkce
2. Lineární funkce
3. Sigmoidní (logistická) funkce
4. Hyperbolický tangens (Tahn)
5. ReLU aktivační funkce
→ Stručné závěry a srovnávací tabulka

Jak fungují neurony

Neuronová síť strukturálně a funkčně kopíruje nervový systém živých organismů. Skládá se z mnoha umělých neuronů, které jsou propojeny ve formě sítí a vrstev. Vzájemně na sebe působí a přenášejí data z mřížky do mřížky a z vrstvy do vrstvy. Díky tomu mohou neurony vykonávat složité úkoly, jako je rozpoznávání obrazů nebo vytváření předpovědí.

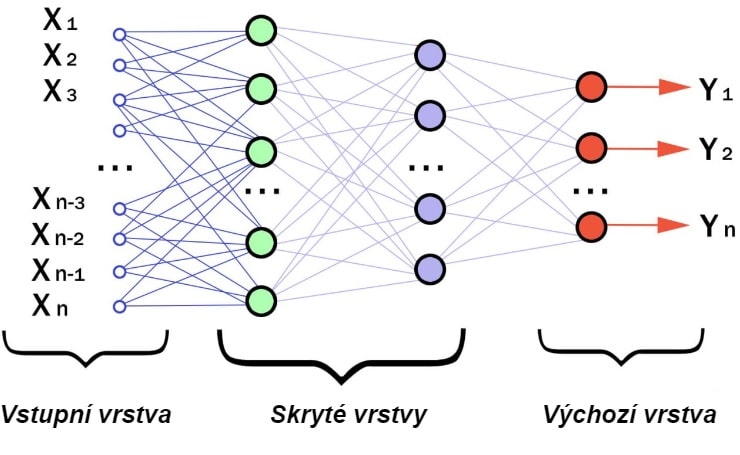
Nejjednodušší schéma neuronové sítě

Základní jednotkou každé neuronové sítě je neuron. Funguje na následujícím principu:

1. Umělý neuron přijímá vstupní hodnoty x_i, což mohou být vektorové nebo číselné hodnoty představující vlastnosti nebo hodnoty předchozích neuronů.

2. Vstupní hodnota se vynásobí příslušnou váhou. Tato váha (wji) určuje důležitost tohoto vstupu pro výpočty neuronu. Hodnoty získané jako výsledek násobení se sečtou:

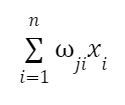
3. K součtu vážených hodnot se přičte zkreslení. Posunutí (bias) v umělém neuronu je dodatečný parametr, určitá konstantní hodnota, díky níž může být neuron aktivován, přestože vážené vstupy dosáhnou nuly.

Důležité! Bez posunutí by neuronová síť mohla reprezentovat pouze lineární zobrazení, což by omezilo její schopnost řešit složité problémy a získávat z dat komplexní vzory.

4. Výsledný součet je převeden přes aktivační funkci, která na vážený součet aplikuje nelineární transformaci. Aktivační funkce určuje výstup neuronu přidáním nelinearit do modelu.

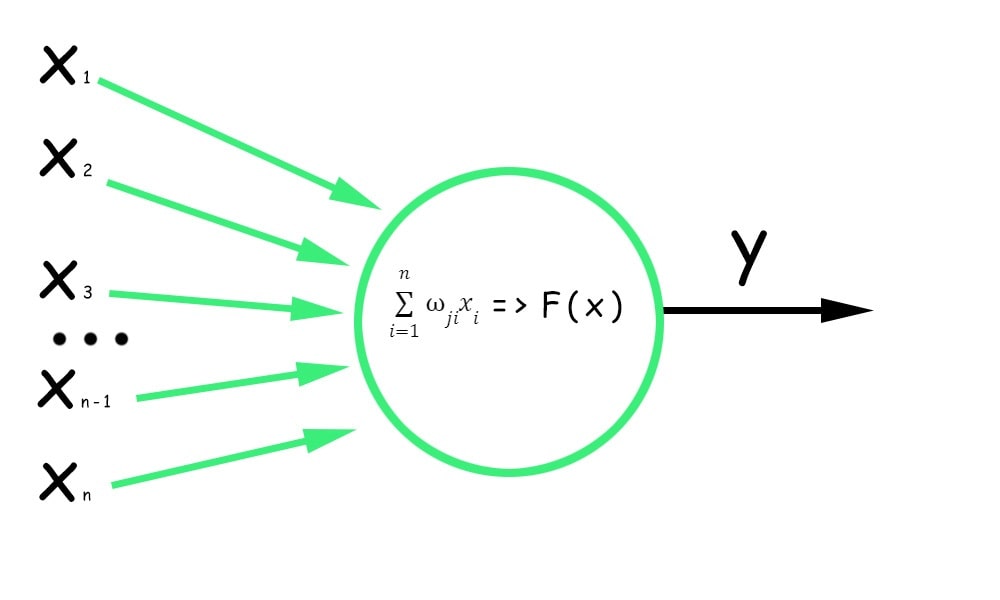
Jak funguje neuron

Všimni si, že offset i aktivační funkce společně ovlivňují aktivaci neuronu. Offset umožňuje nastavit základní úroveň aktivace, zatímco aktivační funkce určuje, jak se bude aktivace neuronu měnit v závislosti na vstupech a offsetu.

Ve skrytých vrstvách neuronové sítě se obvykle (ne vždy, ale nejčastěji) používá stejná aktivační funkce neuronu. U výstupní vrstvy se aktivační funkce mírně mění.

Prahová (skoková) funkce

Nejjednodušší aktivační funkce. Někdy se nazývá Gavisideova funkce. Pokud hodnota krokové funkce překročí určitou mez, považuje se neuron za aktivovaný:

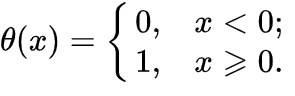
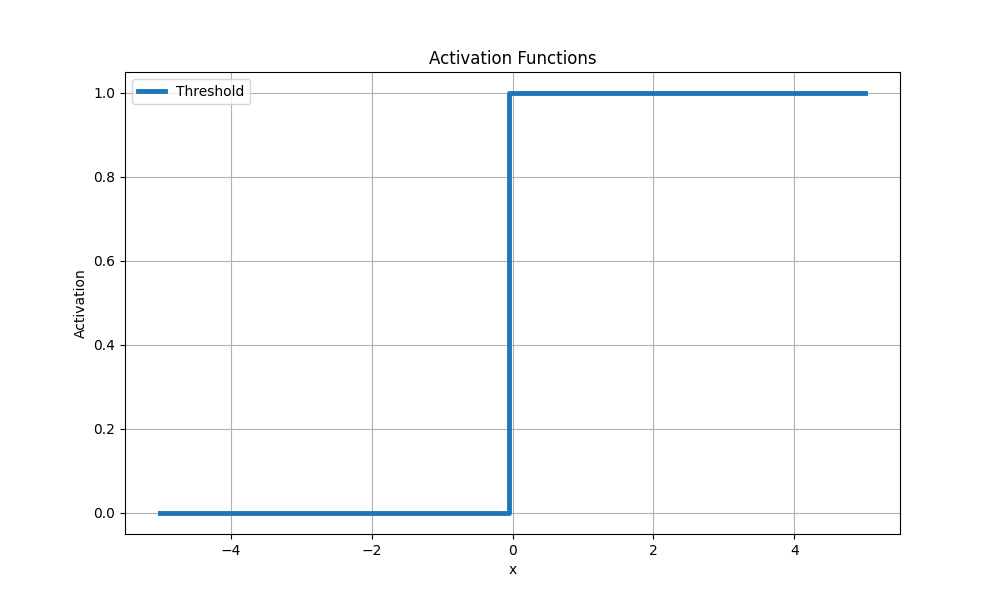
Prahová (skoková) aktivační funkce

Nevýhody

Prahová funkce je spojitá a nediferencovaná, což vede ke dvěma problémům, kvůli kterým se tato funkce v neuronových sítích pro hluboké učení téměř nepoužívá:

1. První problém souvisí s algoritmem zpětného šíření chyby Backpropagation, což je mechanismus trénování neuronových sítí. Ten upravuje váhy spojení mezi neurony v síti na základě vypočtených chyb předpovědi.

Gradient potřebný k aktualizaci vah během trénování sítě lze vypočítat pouze s diferencovatelnými aktivačními funkcemi (gradient se vypočítá pomocí derivace aktivační funkce ze vstupu neuronu).

2. Druhým problémem jsou skoky v aktivační funkci Gaviside. Ty vedou ke spojitým změnám výstupních hodnot neuronů při malých změnách vstupních dat. V důsledku toho se síť může "zaseknout" v určitých částech neuronové sítě, kde výstupní hodnoty neuronů přeskakují mezi dvěma různými hodnotami.

Tento zádrhel ztěžuje obnovení vah neuronů v těchto oblastech, protože malé změny vah nevedou ke kontinuálním změnám výstupů neuronů. V důsledku toho se síť nemusí pohybovat správným směrem a nemusí dosáhnout optimálních vah.

Lineární funkce

Další nejjednodušší aktivační funkce, u níž změny vstupního signálu proporcionálně ovlivňují výstup bez nelineárních transformací:

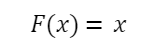
Lineární aktivační funkce

V tomto ohledu je použití lineární funkce omezeno na regresní úkoly, kde je třeba předpovědět spojitou hodnotu. Například v úkolu předpovědi ceny nemovitosti s přihlédnutím k různým funkcím ji lze použít na původní vrstvu.

Funkci lze použít i na jednotlivé vrstvy lineární sítě, které provádějí lineární operace na vstupech. V tomto případě aktivační funkce snadno přenáší hodnoty bez nelineárních transformací.

Příklad použití

Představme si, že řešíme problém předpovědi prodeje zboží na základě nákladů na jeho reklamu.

Máme:

• informace o částkách vynaložených na reklamu v různých mediálních kanálech (propagace v televizi/rádiu, sociální média);
• odpovídající informace o objemu prodeje zboží

Konečným cílem tohoto úkolu je sestavit model, který by na základě vstupních dat předpovídal prodeje.

Použijme neuronovou síť s jednou lineární vrstvou a lineární aktivační funkcí. 

Vstupními daty budou hodnoty nákladů na reklamu v různých kanálech a výstupními daty bude předpovídaný objem prodeje.

Neuronová síť s lineární aktivační funkcí vytvoří lineární vztah mezi výdaji na reklamu a tržbami. Model se bude snažit najít optimální váhy pro jednotlivé reklamní kanály, aby na základě údajů o nákladech co nejlépe předpověděl prodeje.

Nevýhody

Lineární aktivační funkce je vhodná pouze pro jednoduché modely nebo jako poslední vrstva v neuronové síti pro řešení regresních úloh, kde je třeba předpovědět číselnou hodnotu.

Sigmoidní funkce (logistická)

Logistická funkce je nelineární a komprimuje vstupní hodnoty od 0 do 1 podle vzorce:

kde x je vstupní hodnota.

Nejčastěji se sigmoidní aktivační funkce používá v úlohách binární klasifikace, kde je třeba předpovědět možnost příslušnosti k jedné ze dvou tříd. Převádí vstupní hodnoty na pravděpodobnosti, které lze interpretovat jako pravděpodobnost příslušnosti k pozitivní třídě.

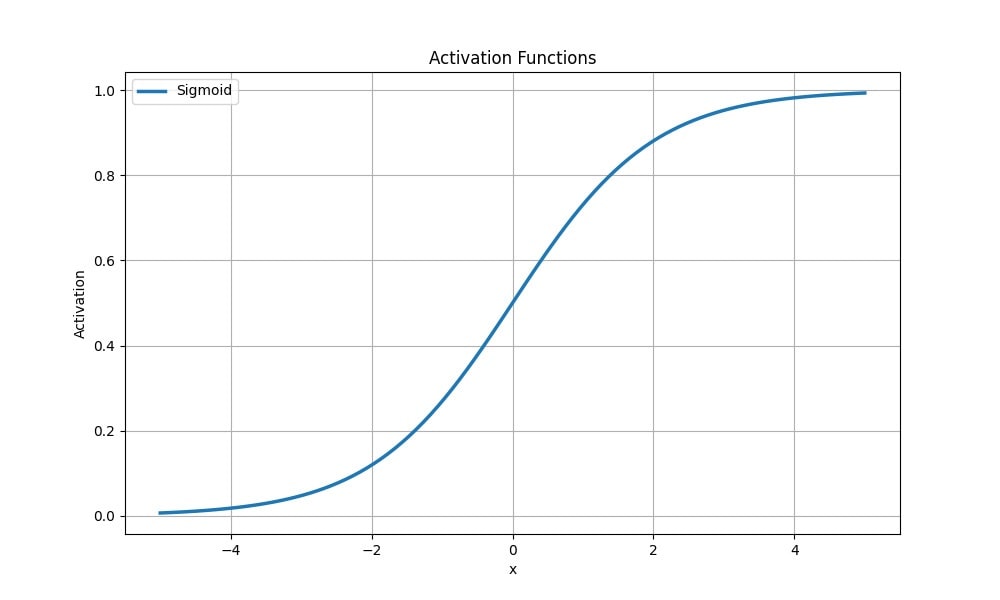
Sigmoidální aktivační funkce

Příklad použití

Představme si, že máme soubor dat, který se skládá z fyzických charakteristik pacientů. Potřebujeme vytvořit model, který bude předpovídat, zda má pacient srdeční onemocnění.

K tomu můžeme použít neuronovou síť s jedním výstupním neuronem a sigmoidální aktivační funkcí:

• vstupní údaje mohou zahrnovat věk pacienta, hladinu cholesterolu, krevní tlak a další charakteristiky;
• výstupní neuron předpoví pravděpodobnost srdečního onemocnění.

Sigmoidní aktivační funkce převádí vážený součet vstupních hodnot a vah na pravděpodobnost. Pokud je například výstupní hodnota sigmoidní funkce 0,89, znamená to, že model předpovídá přítomnost kardiovaskulárního onemocnění s pravděpodobností 89 %.

Nevýhody logistické funkce

V oblasti silně kladných nebo záporných hodnot se derivace logistické funkce stává malou. To vede v případě zpětného šíření chyby k efektu útlumu gradientu a jeho malé hodnotě, což je pro obnovu neuronových vah a trénování hlubokých neuronových sítí s velkým počtem vrstev krajně neefektivní.

Hyperbolický tangens (Tahn)

Úplný vzorec pro hyperbolický tangens (tanh) je následující:

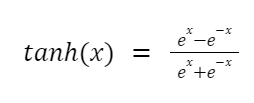
Ale protože chování tangens je podobné sigmoidě, lze jej představit takto:

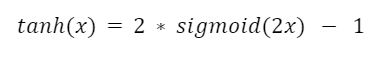
Tangens má se sigmoidou společné i slabé stránky: obě jsou nelineární a kompresní a obě jsou omezeny v rozsahu od -1 do 1.

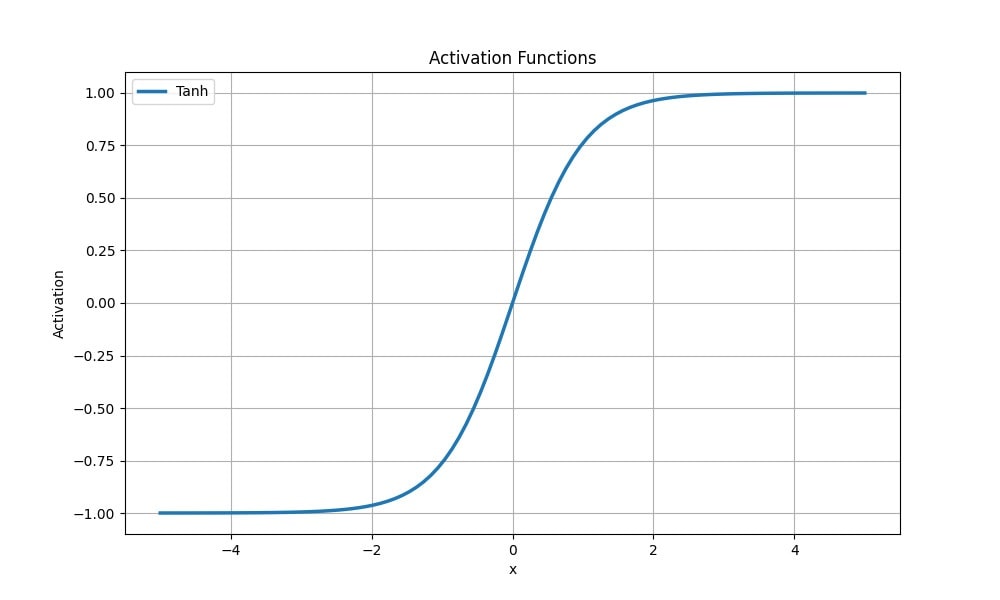
Hyperbolický tangens

Současně (ve srovnání se sigmoidální aktivační funkcí) má tanh(x) výraznější gradient v blízkosti nuly. To může být užitečné při modelování dat, která mají symetrické rozdělení kolem nuly a jejichž záporné hodnoty je důležité zachovat.

Nevýhody hyperbolického tangens

Nevýhody tanh(x) souvisejí také s problémem oslabení gradientu.

Při použití backpropagation se lokální gradient vypočítá vynásobením derivací aktivačních funkcí vrstev neuronové sítě. Maximální derivace hyperbolického tangens je vždy menší než jedna a vypočítá se podle vzorce:

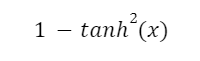
Maximální hodnota derivace logistické aktivační funkce v bodě 0 je ¼ a vypočítá se takto:

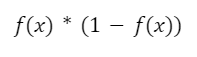
Při násobení derivací aktivačních funkcí pro n vrstev bude maximální lokální gradient s každou vrstvou klesat a bude mít hodnotu 1/(2n). Pokud se počet vrstev v modelu sítě zvýší a lokální gradient se odpovídajícím způsobem sníží, mohou váhy v prvních vrstvách zůstat prakticky nezměněny, protože gradient se stane velmi malým.

Vzhledem k rozpadu gradientu v počátečních vrstvách budou aktualizace vah probíhat především v hlubších vrstvách a učení bude probíhat od konce neuronové sítě. V důsledku aktivace sedmé až osmé vrstvy získáme menší příspěvek k celkovému procesu učení ve srovnání s hlubšími vrstvami, kde se gradienty udržují na vyšších hodnotách.

Závěr: Logistická aktivační funkce (sigmoida) i hyperbolický tangens se pro hluboké neuronové sítě často nedoporučují, zejména při použití velkého počtu vrstev.

Příklad použití hyperbolického tangens

Podívejme se na úkol z kategorie předpovědí časových řad (časová řada je posloupnost dat uspořádaná podle času). Předpokládejme, že máte k dispozici údaje o teplotě vzduchu za určité časové období a potřebujete sestavit model, který bude předpovídat teplotu následujícího dne.

Používáme rekurentní neuronovou síť (RNN) s aktivační funkcí tanh(x). RNN má paměť, která jí umožňuje zohlednit předchozí hodnoty a na základě této historie předpovídat budoucí hodnoty.

Kód v jazyce Python používající rámec TensorFlow bude vypadat přibližně takto:

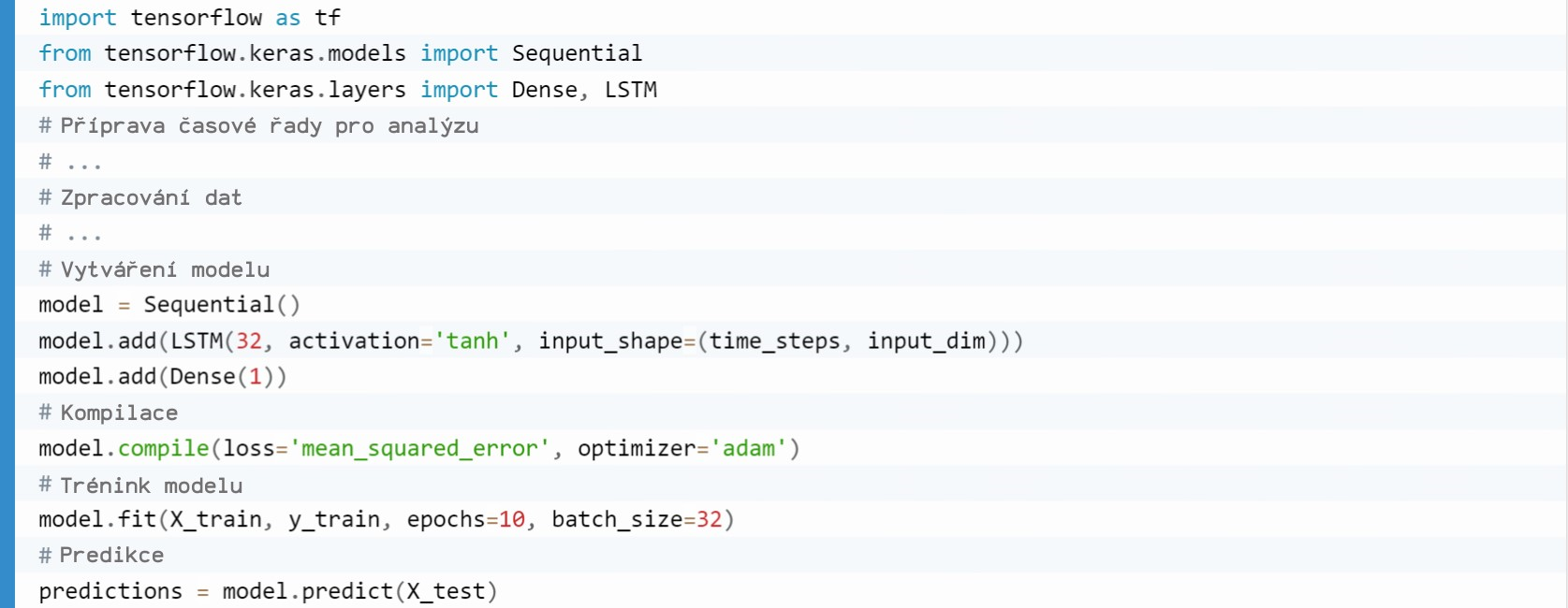
Důležité! Tento kód předpokládá, že data jsou již optimalizována a připravena k použití.

Obecný princip budování neuronové sítě je následující:

• Pomocí funkce Sequential() se vytvoří sekvenční model neuronové sítě.
• Metoda model.add() přidá vrstvu LSTM (s 32 skrytými neurony a aktivační funkcí hyperbolický tangens).
• Parametr input_shape=(time_steps, input_dim) definuje velikost vstupu modelu, kde time_steps je počet časových kroků a input_dim je počet prvků v každém časovém kroku.
• Model se zkompiluje pomocí příkazu model.compile(). Určuje ztrátovou funkci mean_squared_error a optimalizátor adam, který se používá k aktualizaci vah modelu.
• Pomocí trénovací metody model.fit() natrénujeme model na trénovacích datech (X_train, y_train).
• Zadáme počet epoch epochs=10 (určuje, kolikrát celá sada trénovacích dat projde během trénování neuronovou sítí) a velikost dávky dat použité pro každou aktualizaci váhových koeficientů – batch_size=32.
• Po dokončení trénování použijeme model.predict() na testovací data (X_test), abychom získali předpovězené hodnoty.

Aktivační funkce ReLU

ReLU (Rectified Linear Unit) je jednou z nejoblíbenějších aktivačních funkcí používaných v nízkovrstvých sítích i v modelech hlubokého učení.

Vzorec ReLU:

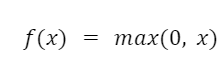
kde x je vstupní signál a f(x) je výstupní signál.

Aktivační funkce ReLU

Tato aktivační funkce (a její stávající modifikace) eliminuje problém mizejícího gradientu. Gradienty pro hodnoty větší než nula zůstávají nenulové, což zajišťuje efektivní šíření gradientů a aktualizací vah během trénování.

Co je dobré vědět: Upravené funkce Leaky ReLU, Parametric ReLU (PReLU) a Exponential Linear Unit (ELU) mají také vlastnosti, které pomáhají zabránit rozpadu gradientu. Například Leaky ReLU přidává malý sklon pro záporné hodnoty a ELU má exponenciální závislost pro záporné hodnoty.

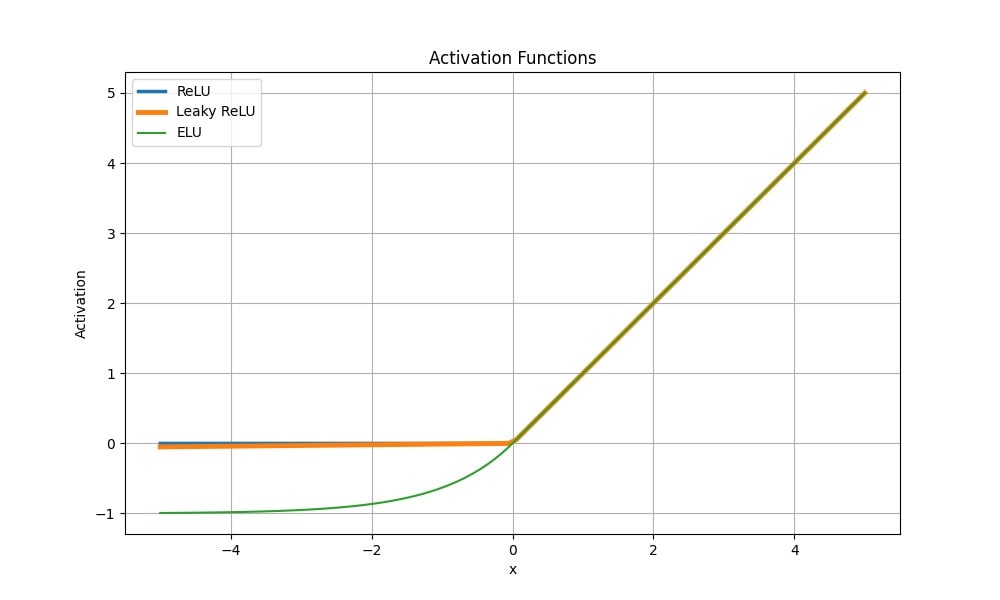
Srovnání aktivační funkce ReLU s jejími modifikacemi

Ačkoli graf ukazuje částečnou linearitu, funkce ReLU je nelineární a její kombinace jsou také nelineární.

Funkce je univerzální a vhodná pro jakýkoli úkol, aniž by vyžadovala velký výpočetní výkon. Funkce nahrazuje všechny záporné hodnoty nulou a kladné hodnoty předává beze změny. Gradienty pro kladné hodnoty zůstávají nenulové, což umožňuje efektivně šířit gradienty a aktualizovat váhy během trénování.

Funkce ReLU aktivuje pouze některé neurony a ostatní ponechává neaktivní. To umožňuje síti učit se z řidších reprezentací dat a snižuje riziko nadměrného učení.

Nevýhody funkce ReLU

Zřejmou nevýhodou aktivační funkce ReLU je její nenormalizace. Stejně jako sigmoidní aktivační funkce je výstupní hodnota ReLU vždy v rozsahu od 0 do ∞, což může být v některých případech omezující.

Jak problém vyřešit: Před použitím aktivační funkce ReLU data normalizujte.

Kvůli velkým váhovým hodnotám nebo nevyváženým datům se u ReLU (nemodifikované verze) může vyskytnout problém „mrtvých neuronů“, který snižuje výkon v modelech hlubokého učení. To znamená, že pokud jsou váhy pro určité vstupy záporné nebo blízké nule, funkce ReLU aktivuje neuron pouze pro kladné hodnoty vstupů, zatímco ostatní zůstanou pasivní.

Závěr

Aktivační funkce určuje výstupní signál neuronu na základě jeho vstupu. Jednoduše do ní dosadíme součtovou hodnotu součinu vstupních signálů neuronu a váhových koeficientů a získáme výstupní signál neuronové sítě.

Níže jsou uvedeny výhody a nevýhody různých aktivačních funkcí:

• Prahová funkce je binární a používá se jen zřídka kvůli své spojitosti a absenci gradientu.
• Lineární aktivační funkce přenáší vstupní signál beze změny, proto se používá v jednoduchých modelech a není vhodná pro reprezentaci složitých nelineárních závislostí.
• Hyperbolický tangens (tanh) komprimuje vstupní hodnoty v rozsahu od -1 do 1. Často se používá ve skrytých vrstvách neuronových sítí k zachování záporných hodnot a zajištění nelinearity.
• Sigmoida transformuje vstupní hodnoty v rozsahu od nuly do jedné. Často se používá v klasifikačních úlohách, ale při trénování hlubokých neuronových sítí trpí problémem tlumeného gradientu.
• ReLU (Rectified Linear Unit) aktivační funkce aktivuje neuron, pokud je vstup kladný, jinak je výstupem 0. Je široce používána v hlubokých neuronových sítích díky své jednoduchosti a absenci tlumeného gradientu, ale může způsobit „mrtvé neurony“ se záporným vstupem.

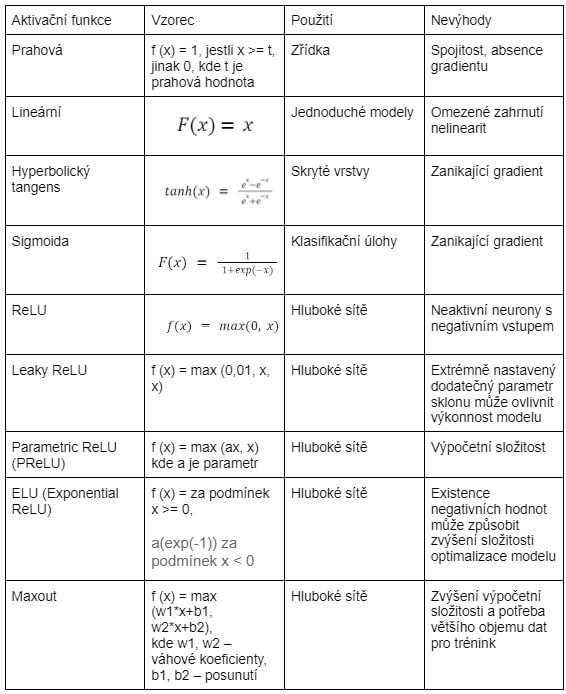
Na závěr uvádíme tabulku porovnávající hlavní aktivační funkce a některé modifikace ReLU. Uložte si ji, abyste ji měli po ruce:

Autor: Serhii Bondarenko