Co je rozdělení pravděpodobnosti?

Číslo hozené na kostce, věk kolemjdoucího, doba čekání na letadlo – to jsou náhodné veličiny. Setkáváme se s nimi i v naší práci. Kolik lidí dnes navštíví webové stránky, jaké příjmy bude mít společnost tento měsíc – to nelze předem zjistit.

V teorii pravděpodobnosti je náhodná veličina proměnná, která může nabývat různých možných hodnot v závislosti na konkrétním případu.

Rozdělení pravděpodobnosti je zákon, který popisuje hodnoty náhodné veličiny a pravděpodobnosti jejich výskytu.

Ve skutečnosti jsou náhodné proměnné často složité. Matematika však dokázala určit vzorce jejich chování. Podívejme se na ty hlavní.

Rovnoměrné rozdělení

Klasickým příkladem je hod mincí. Je to náhodná proměnná se dvěma výsledky – hlava nebo orel. Předpokládejme, že pravděpodobnost, že padne hlava nebo orel, je rovna 1/2.

Nyní si vezměte šestistěnnou hrací kostku. Číslo, které na ní padne, je náhodná veličina, která nabývá hodnot od 1 do 6 s pravděpodobností 1/6.

Obdobný zákon bude fungovat, i když zvolíme libovolné číslo – například číslo losu. Dostáváme se k náhodné veličině, která nabývá deseti různých hodnot (od 0 do 9), přičemž každá z nich nabývá pravděpodobnosti 1/10.

V obecném případě máme libovolný počet výsledků. Dostáváme se tak k náhodné proměnné, která nabývá n hodnot {1,2,3,…,n}, každou s pravděpodobností 1/n. Toto rozdělení se nazývá diskrétní rovnoměrné rozdělení. Jeho pravděpodobnostní funkce se bez ohledu na konkrétní hodnotu rovná:

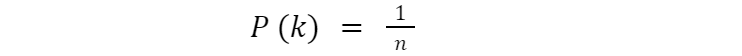
Graf takové pravděpodobnostní funkce na nějakém úseku [a, b] bude vypadat takto:

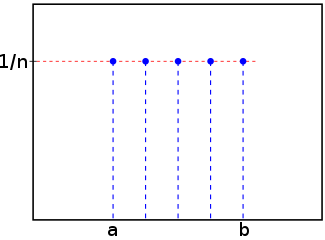
Zdroj: Wikipedie

Kromě pravděpodobnostní funkce je s náhodnou veličinou spojen další objekt. Ke zjištění, s jakou pravděpodobností bude hodnota náhodné veličiny menší nebo větší než nějaké číslo, se používá distribuční funkce. Jedná se o pravděpodobnost, že náhodná veličina bude menší nebo rovna libovolné hodnotě P(Xk). Pravděpodobnost, že mezi objekty {1,..., n} získáme hodnotu menší nebo rovnou k, je k/n. Dostaneme tedy distribuční funkci F(k)=k/n.

Zde je její graf:

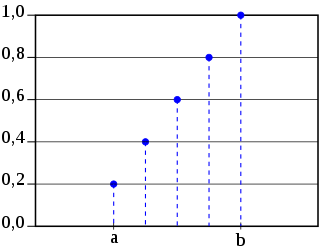
Zdroj: Wikipedie

V diskrétním modelu je počet možných hodnot náhodné proměnné konečný. Uvažujme problém se spojitým rozdělením. Na nástupiště se člověk dostane se stejnou pravděpodobností kdykoli. Na toto nástupiště přijíždí vlak každých 30 minut. Je třeba si uvědomit, jaká je pravděpodobnost, že budete na vlak čekat déle než 20 minut.

Tento úkol vede ke konceptu rovnoměrného spojitého rozdělení. Čekání na vlak je zde náhodná veličina, která bude nabývat hodnot v rozmezí od 0 do 30. Pravděpodobnost získání libovolné číselné hodnoty v rozmezí od 0 do 30 je konstantní. Hustota distribuce tedy bude konstanta. Tato konstanta by měla být taková, aby velikost plochy pod grafem hustoty byla rovna jedné.

V našem případě bude hustota pravděpodobnosti 1/30. V obecném případě je to 1/(ba).

Graf:

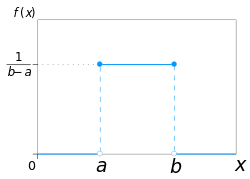
Zdroj: Wikipedie

Distribuční funkce F(x) je pravděpodobnost čekání na vlak od a do x minut. Vypočítáme ji jako plochu pod grafem z bodu a do bodu x funkce hustoty f. To je F(x)=x/30 a v obecném případě F(x)=(x-a)/(b-a).

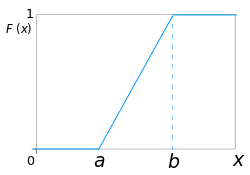
Zdroj: Wikipedie

Jak vidíte, distribuční funkce je integrálem hustoty distribuce.

K vyřešení úlohy potřebujeme vypočítat hodnotu P(x>20). Lze ji zjistit jako plochu obdélníku o šířce 10 (od 20 do 30) a výšce 1/30. Lze ji také definovat jako hodnotu 1-F(20). V obou případech je odpověď ⅓. Pravděpodobnost čekání delšího než 20 minut je ⅓.

Všechny hodnoty rovnoměrného rozdělení v daném rozsahu jsou stejně pravděpodobné.

Bernoulliho rozdělení

O rovnoměrném rozdělení jsme už psali u klasického pokusu s mincí, kde byla pravděpodobnost obou výsledků stejná. Ale co když uvažujeme minci, kde padne hlava s pravděpodobností p a orel s pravděpodobností q?

Náhodná veličina se 2 výsledky nabývá hodnoty 1 s pravděpodobností p a hodnoty 0 s pravděpodobností q tak, že p+q=1.

Toto rozdělení lze použít i v životě. Pokud jste dobře připraveni, máte větší šanci, že zkoušku složíte, než že ji nesložíte. Zkušený střelec spíše zasáhne cíl, než mine.

Zde je pravděpodobnostní funkce takového rozdělení:

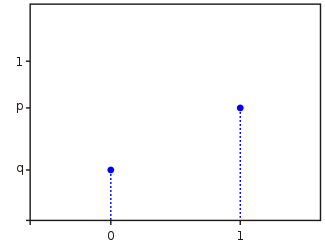
Zdroj: Wikipedie

Náhodná veličina má 2 hodnoty - 0 a 1. Její distribuční funkce je však definována pro všechna reálná čísla:

Náhodná veličina nemůže mít nikdy hodnotu menší než nula - nabývá pouze hodnot 0 a 1. F(x)=0 pro všechna x<0.

Hodnota 0 bude podle definice pravděpodobnosti q. F(0)=q.

Najdeme F(x)=P(X<x) pro 0<x<1. Náhodná veličina nenabývá hodnoty 0<x<1. Jediná hodnota menší než takové x je 0. Pravděpodobnost P(X<x) pro 0<x<1 je tedy P(X=0). Pak F(x) pro libovolné 0<x<1 je F(0) : F(x)=F(0)=q.

Zjistíme pravděpodobnost, že dostaneme hodnotu menší nebo rovnou 1. Protože náhodná veličina nabývá pouze dvou hodnot a obě jsou <=1, je tato pravděpodobnost rovna 1: P(X<=1)=P(X=0 nebo X=1)=1.

Totéž platí pro libovolné x>1 : P(x)=P(1)=1. 

Graf F(x):

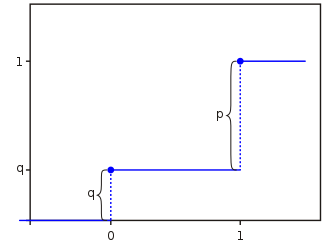
Zdroj: Wikipedie

Binomické rozdělení

Stává se, že se nezvažuje jeden test, ale několik testů za sebou.

Stává se, že se neuvažuje o jednom procesu, ale o několika procesech po sobě jdoucích.

O tom, zda je pacient nemocný, rozhoduje například skupina lékařů. Dva lékaři se domnívají, že ano, a jeden, že ne.

Model telefonu může mít různé vady. Při kontrole se ukázalo, že jeden telefon má vady na displeji a v baterii a ten druhý pouze v baterii.

Odhadněme teď pravděpodobnost takových událostí. Předpokládejme, že pravděpodobnost události je v rámci jedné řady stejná. Předpokládejme tedy, že se stejnou pravděpodobností p se každý z lékařů rozhodne kladně a že pravděpodobnost výskytu závad u nového telefonu je vždy stejná.

V těchto případech se provádí série Bernoulliho pokusů: je n experimentů, v každém z nich je pravděpodobnost úspěchu p, pravděpodobnost neúspěchu q. Jak odhadnout pravděpodobnost, že v n pokusech bude přesně k úspěchů?

Uvažujte případ 3 pokusů a zjistěte pravděpodobnost získání 2 úspěchů ze 3. Je-li p pravděpodobnost úspěchu a q pravděpodobnost neúspěchu, pak pravděpodobnosti různých kombinací v těchto pokusech jsou následující:

Pravděpodobnost 3 úspěchů ve 3 pokusech = ppp=p 3

Pravděpodobnost úspěchu v 1. a 2. pokusu a neúspěchu ve 3. pokusu = ppq=p 2 q

Pravděpodobnost úspěchu v 1. a 3. pokusu a neúspěchu ve 2. pokusu = pqp=p 2 q

Pravděpodobnost úspěchu v 1. pokusu a neúspěchu ve 2. a 3. pokusu = pqq=q 2 p

Pravděpodobnost neúspěchu v 1. pokusu a úspěšnost ve 2. a 3. pokusu = qpp=p 2 q

Pravděpodobnost neúspěchu v 1. a 3. pokusu a úspěšnost ve 2. pokusu = qpq=q 2 p

Pravděpodobnost neúspěchu v 1. a 2. pokusu a úspěšnost ve 3. pokusu = qqp=q 2 p

Pravděpodobnost 3 selhání ve 3 pokusech = qqq=q 3

Zajímají nás případy 2 úspěchů a 1 neúspěchu. Existují 3 takové případy a pravděpodobnost každého z nich je p 2 q. Liší se pouze v tom, ve kterém ze tří experimentů byly dva pokusy úspěšné a ve kterém neúspěšné.

Pravděpodobnost 2 úspěchů ze 3 je tedy 3p 2 q.

To, že koeficient je roven 3, není náhoda. Tento počet možností představuje přesně 2 úspěchy ve 3 pokusech, tedy výběr 2 míst ze 3 možných. Počet způsobů, jak vybrat 2 objekty ze 3, je počet kombinací C 2 3 =3.

Obecně se počet způsobů výběru k objektů z n označuje jako Cn k a pravděpodobnostní funkcí binomického rozdělení je pravděpodobnost k úspěchů v n pokusech.

Jaká je pravděpodobnost, že nenastane více než k úspěchů? Odpověď na tuto otázku nám poskytne vzorec distribuční funkce. Je zřejmé, že abyste nezískali více než k úspěchů, musíte získat buď 0 úspěchů, nebo 1, nebo 2,..., k-1, k. Tyto možnosti se vzájemně vylučují, takže pravděpodobnost, že se nepodaří získat více než k úspěchů, je rovna součtu pravděpodobností, že se podaří získat 0 úspěchů, 1,..., k. A my známe každou takovou možnost. Distribuční funkce tedy bude:

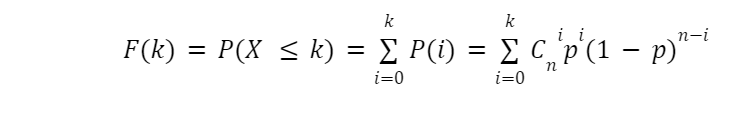
Normální rozdělení

Existují náhodné veličiny, které jsou výsledkem vlivu velkého množství malých nezávislých náhodných faktorů.

Příkladem takových proměnných jsou hodnoty jako výška, hmotnost, krevní tlak, skóre TOEFL nebo výsledek závodu na 100 metrů. Výšku člověka ovlivňuje více než 80 různých genů. Hmotnost je navíc ovlivněna životním stylem, mírou sportovní zátěže a kalorickým příjmem.

Zdá se, že se tyto hodnoty pohybují kolem průměru. Průměrná výška člověka je někde v rozmezí od 160 do 180 cm. Lidé s vyšší nebo nižší tělesnou výškou se v populaci vyskytují méně často. Kromě toho je pravděpodobnost, že potkáte jak velmi vysokou, tak velmi nízkou osobu, přibližně stejná.

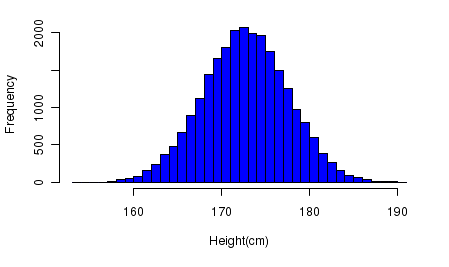
Zdroj: Countbio

Podívejme se na histogram výškových frekvencí souboru více než 25 tisíc osmnáctiletých, získaný na základě údajů statistické agentury SOCR. Vidíme, že nejvyšší frekvence odpovídá průměrné výšce přibližně 172 cm. Samotné rozdělení je obecně symetrické.

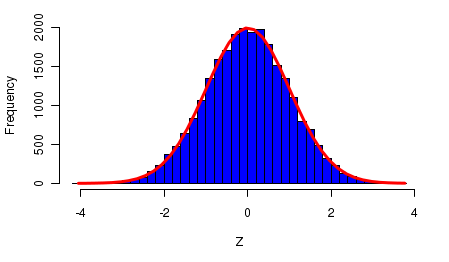
Zdroj: Countbio

Takový graf se blíží křivce připomínající tvar zvonu:

Pokud zvětšíte velikost vzorku, bude graf histogramu stále více připomínat zvonovitou křivku. To je vlastnost všech náhodných veličin, které jsou průměrem řady nezávislých náhodných faktorů (jako v případě výšky nebo hmotnosti).

Takové zvonové rozdělení označujeme jako normální rozdělení.

Toto rozdělení je definováno dvěma parametry – střední hodnotou a rozptylem. Většina hodnot takového rozdělení se nachází kolem jeho středu. Silné odchylky od průměru směrem nahoru nebo dolů jsou nepravděpodobné. Čím větší je odchylka od průměru, tím menší je pravděpodobnost takové události.

Normální rozdělení se střední hodnotou a rozptylem 0 a 1 se nazývá standardní normální rozdělení. Jeho vzorec pro hustotu byl získán jako výsledek určitého mezního procesu a je následující:

Distribuční funkce bude funkcí plochy pod grafem takové křivky (určitý integrál s proměnnou horní hranicí z výše uvedené funkce). K jejímu výpočtu můžete použít speciální tabulky nebo programy.

Autor: Filipov Nikita