Gradientní sestup: algoritmus a příklad v jazyce Python

Gradientní sestup je jedna z optimalizačních metod, která umožňuje neuronové síti učit se. Jak a proč gradientní sestup funguje? Přečti si v našem článku.

Jak se neurony učí a proč potřebujeme gradientní sestup?

Netrénovaná neuronová síť je špatný pomocník: chová se nepředvídatelně a generuje náhodné odpovědi. Pokud jí však řekneme, co je správné a co ne, dokáže předpovídat přesněji než člověk.

Ale jak přesně toho lze dosáhnout?

Ve výchozím nastavení je signál v neuronu přenášen ze vstupních receptorů do první a všech následujících skrytých vrstev, dokud není transformován na signál pro výstupní vrstvu. Dokud však parametry modelu - váhu a zkreslení neuronů - neupravíme, budeme dostávat určité chyby. Abychom je minimalizovali, musíme síť optimalizovat.

Konečným cílem optimalizace je najít hodnoty parametrů, při kterých chybová funkce dosáhne minima.

Jednou z hlavních optimalizačních metod používaných k dosažení tohoto cíle je metoda gradientního sestupu. Pomáhá najít směr, ve kterém se chybová funkce snižuje, a podle toho aktualizovat parametry modelu.

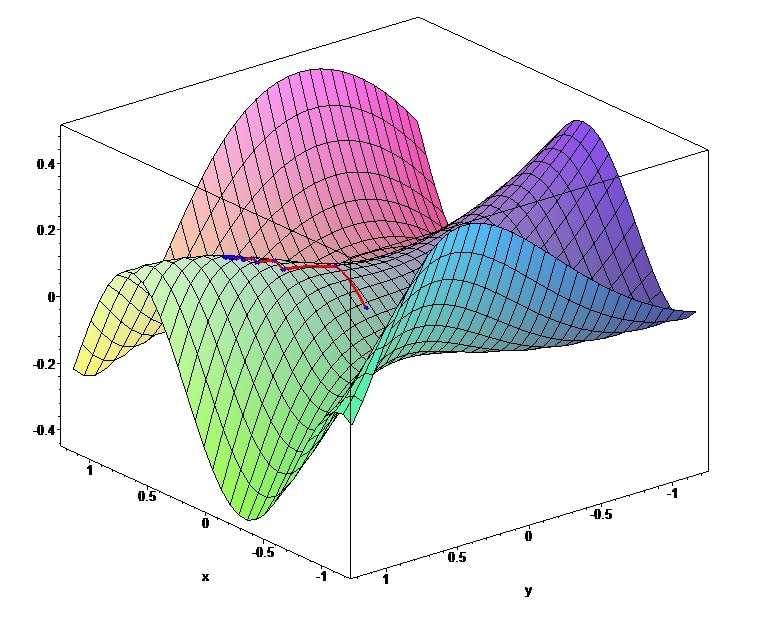
Gradientní sestup

Abychom pochopili podstatu metody, připomeňme si matematiku.

Gradient je vektor, který směřuje ve směru maximální změny funkce.

V kontextu neuronových sítí pomáhá gradient chybové funkce určit, jak změna parametru ovlivní hodnotu chybové funkce. Jinými slovy udává, jak by se měly změnit parametry modelu, aby byla chyba menší.

Metoda využívá gradientní vektor k určení směru, ve kterém chybová funkce klesá nejrychleji. To nám umožňuje "descend the error gradient", jak se blížíme k minimální hodnotě funkce. Parametry modelu se aktualizují při každé iteraci a pohybují se v opačném směru, než je gradient chybové funkce, dokud nenajdeme bod v prostoru parametrů, kde je chyba na trénovacích datech minimální.

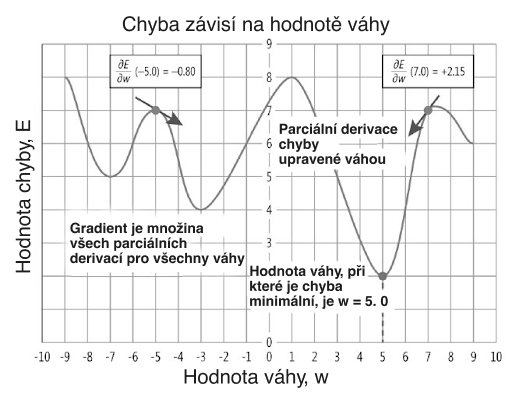
Na začátku s určitými počátečními hodnotami parametrů vypočítáme gradient chybové funkce nad těmito parametry. Poté změníme hodnoty parametrů odečtením určitého zlomku gradientu. Postup opakujeme, dokud nejsou hodnoty parametrů optimální nebo dokud se chybová funkce nepřestane výrazně snižovat.

Algoritmus gradientního sestupu

Matematicky si lze gradientní sestup představit takto:

1. Inicializuj parametry modelu náhodnými hodnotami.

2. Zadej vstupní data do modelu a získej předpověď.

3. Vypočítej hodnotu chybové funkce porovnáním předpovědí se skutečnými hodnotami. Jak přesně to provedete, závisí na dané úloze. Například u regresních úloh můžeš použít vzorec:

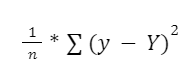
kde n je počet příkladů v trénovací množině, y je skutečná hodnota a Y je předpovídaná hodnota cílové proměnné.

4. Urči gradient chybové funkce pro každý parametr modelu. Vzorec se volí v závislosti na zvolené chybové funkci.

5. Aktualizuj hodnoty parametrů pomocí vzorce:

nová hodnota parametru = stará hodnota parametru - learning rate* gradient.

Learning rate je hyperparametr, který řídí rychlost konvergence algoritmu gradientního sestupu a určuje velikost kroku, s jakou jsou aktualizovány parametry modelu. Čím menší je krok, tím déle trvá trénování neuronové sítě a aktualizace parametrů.

6. Opakuj kroky 2-5 pro každou fázi tréninkového cyklu (epochu) nebo do dosažení kritéria zastavení.

Příklad korekce vah neuronové sítě

Předpokládejme, že máme plně propojenou dopřednou (feed-forward) neuronovou síť. Má náhodně zvolené váhy spojení, které leží v rozsahu [-0,5;0,5].

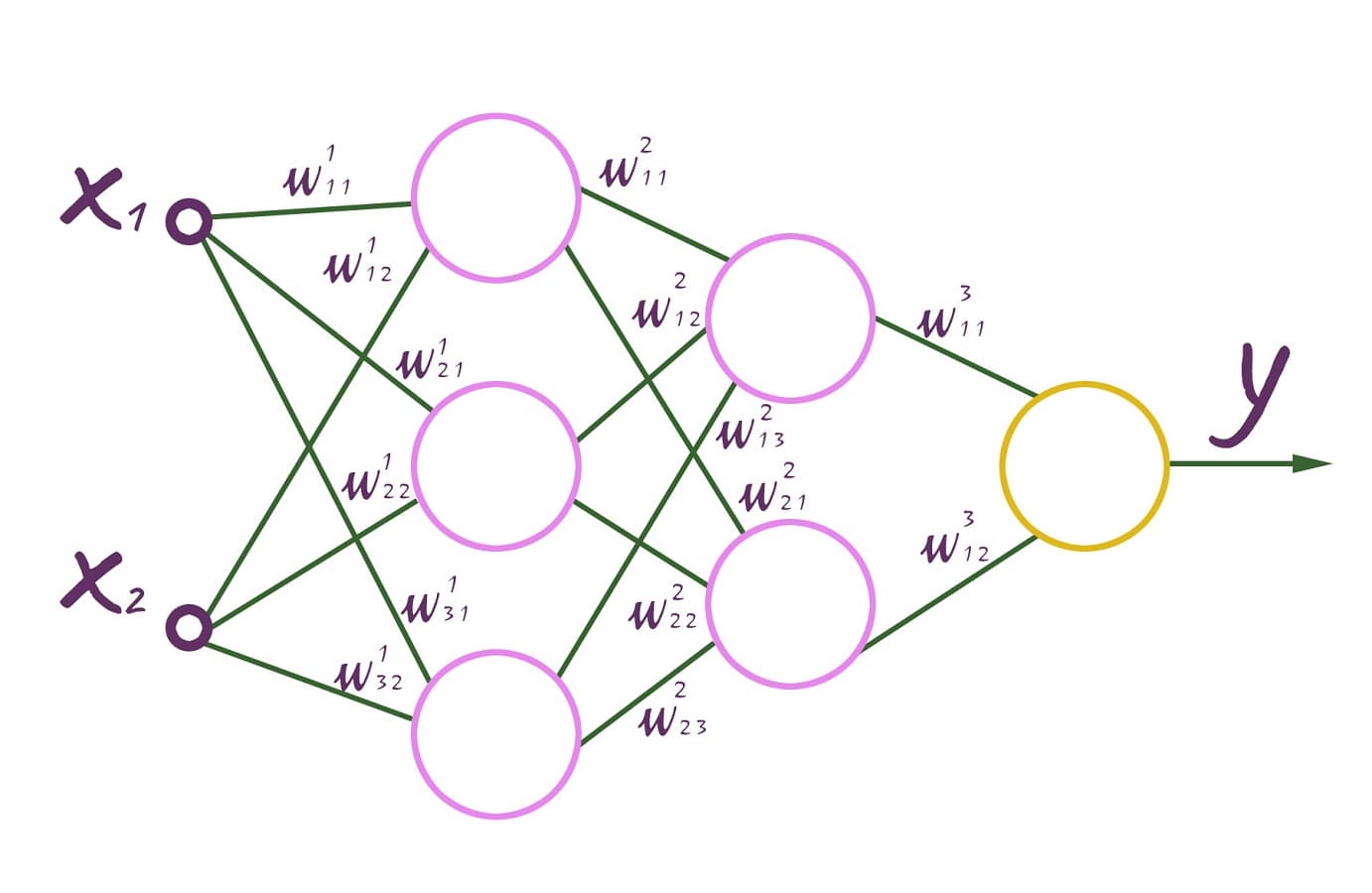
Plně propojená dopředná neuronová síť

Vrchní index znamená příslušnost k určité vrstvě. Každý neuron má aktivační funkci f(x). Každé pozorování má svou vlastní odezvu d.

Procházením této sítě získáme vektor pozorování:

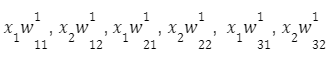
Pro první uzel první vrstvy dostaneme:

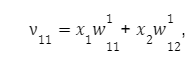
pro druhou:

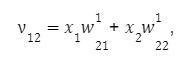
pro třetí:

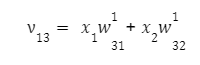
Při průchodu sítí bude mít výstup neuronu určitou hodnotu získanou pomocí aktivační funkce. Ta se vypočítá podle vzorce:

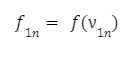
Při dalším pohybu podél sítě získáme vektor pozorování:

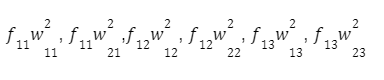
Pro každý neuron druhé vrstvy:

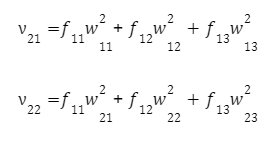
Na prvním neuronu druhé vrstvy:

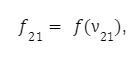
na druhém:

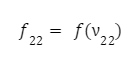
Podobně dojdeme k výstupní hodnotě y. Protože známe požadovanou výstupní hodnotu pro náš vektor x1 a x2 - d, je snadné vypočítat výstupní chybu:

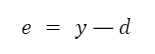
V tomto momentu začíná proces úpravy hmotnosti. Probíhá v opačném směru, od výstupu ke vstupu. Podle algoritmu zpětného šíření musíme vypočítat lokální gradient výstupního neuronu. To se provádí podle vzorce:

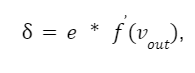
kde f(vout) je derivace aktivační funkce výstupního neuronu.

Výstupní aktivační funkce může být buď hyperbolický tangens, nebo sigmoida.

Přečti si také kompletního průvodce aktivačními funkcemi neuronových sítí.

Tyto funkce jsou rozdílné pouze v úrovni (pro hyperbolický tangens je to rozsah od -1 do 1 a pro logistickou funkci rozsah od -0,5 do 0,5).

Představme si, že jsme vybrali funkci:

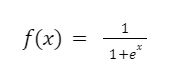
Její derivát bude vypadat takto:

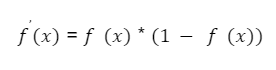
Lokální gradient lze definovat jako:

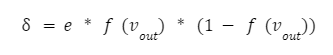
Pokud se podíváme na vzorec, zjistíte, že výstupní hodnota posledního neuronu f(vout) je y, tj. hodnota aktivační funkce součtu vout. Vzorec se tedy stává jednoduchým:

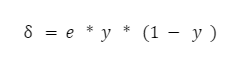
Nyní máme vše, co potřebujeme k výpočtu korekce váhy pro poslední vrstvu. Vypočítáme je podle následujícího vzorce:

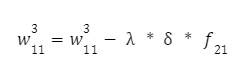
A druhá váha:

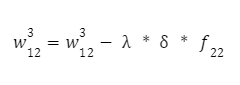
Parametr λ představuje krok trénování neuronové sítě. Čím je menší, tím pomalejší bude proces trénování sítě. Volí se experimentálně (například 0,1, 0,01, 0,001 atd.), dokud není výsledek uspokojivý.

Poté přejdeme na další vrstvu od konce vrstvy - a i pro tyto neurony zopakujeme postup korekce vah stejnou metodou. Vypočítáme hodnoty jejich lokálních gradientů:

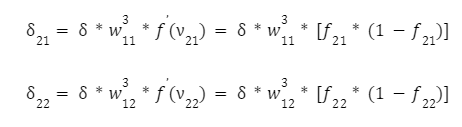
Dále upravíme vstupní spojení těchto neuronů pomocí známého vzorce s krokem trénování neuronové sítě. Pro první z nich:

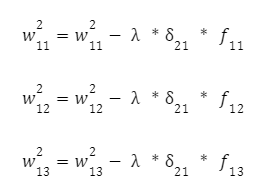
A pro další neuron:

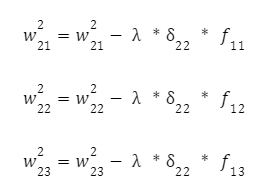
Potřebujeme nyní upravit váhy první vrstvy. Opět vypočítáme lokální gradient první skryté vrstvy. Protože neurony mají dva výstupy, vypočítáme nejprve vážený součet jednotlivých výstupů:

A poté tyto částky vynásobíme derivací aktivační funkce:

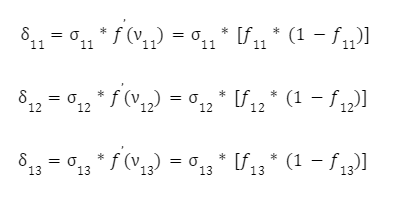
Zbývá pouze upravit váhu první vrstvy:

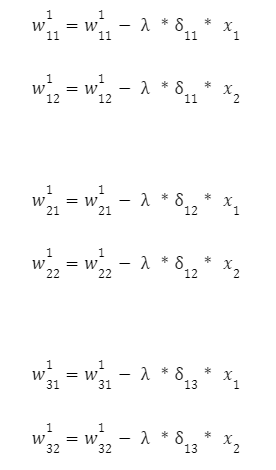
První iteraci algoritmu jsme dokončili úpravou všech vah neuronové sítě. Pro provedení druhé, třetí a dalších iterací je třeba vzít další trénovací vektor vstupních hodnot (x1, x2) a síť spustit znovu. S každým dalším průchodem budou váhy upravovány stále přesněji.

Cílem algoritmu gradientního sestupu je minimalizovat kritérium kvality neuronové sítě - součet čtvercových chyb trénovací množiny:

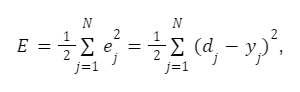
kde N je počet iterací.

Trénování neuronové sítě v jazyce Python

Níže uvedený kód představuje jednoduchou neuronovou síť s jednou skrytou vrstvou, která je trénována pomocí gradientního sestupu. Funguje takto:

• Připojení knihovny NumPy pro práci s poli.
• Definuj dvě funkce: f(x) a df(x). První je sigmoidální aktivační funkce, druhá počítá derivaci této funkce.
• Nastavíme váhové matice W1 a W2 (váhy mezi vstupní a skrytou vrstvou a mezi skrytou a výstupní vrstvou).
• Definuj funkci go_forward(inp), která provádí přímé šíření signálu sítí. Vstupní signál (inp) se vynásobí váhovou maticí W1, aplikuje se aktivační funkce, poté se výsledek vynásobí váhovou maticí W2 a znovu se nechá projít aktivační funkcí. Vrátí se výstupní hodnota neuronové sítě y a aktivační hodnota skryté vrstvy out.
• Definujeme funkci train(epoch), která trénuje neuronovou síť. Uvnitř této funkce se váha iterativně aktualizuje pomocí gradientního sestupu. Pro každý tréninkový cyklus je vybrán náhodný vstupní signál x z epoch tréninkového vzorku. Poté se signál šíří sítí pomocí funkce go_forward, vypočítá se chyba e mezi výstupem a očekávanou hodnotou a pomocí derivace aktivační funkce se určí gradienty. Pomocí vzorců pro gradientní sestup aktualizujeme váhy W2 a W1.
• Vygenerujeme epoch trénovacího vzorku, což je sada vstupních a výstupních hodnot pro trénování sítě.
• Zavoláním funkce train(epoch) natrénuj neuronovou síť na daném vzorku.
• Poté se signál šíří přímo trénovanou sítí pro každý prvek v epoch tréninkového vzorku a zobrazí se výstupní hodnota neuronové sítě y a očekávaná hodnota x[-1].

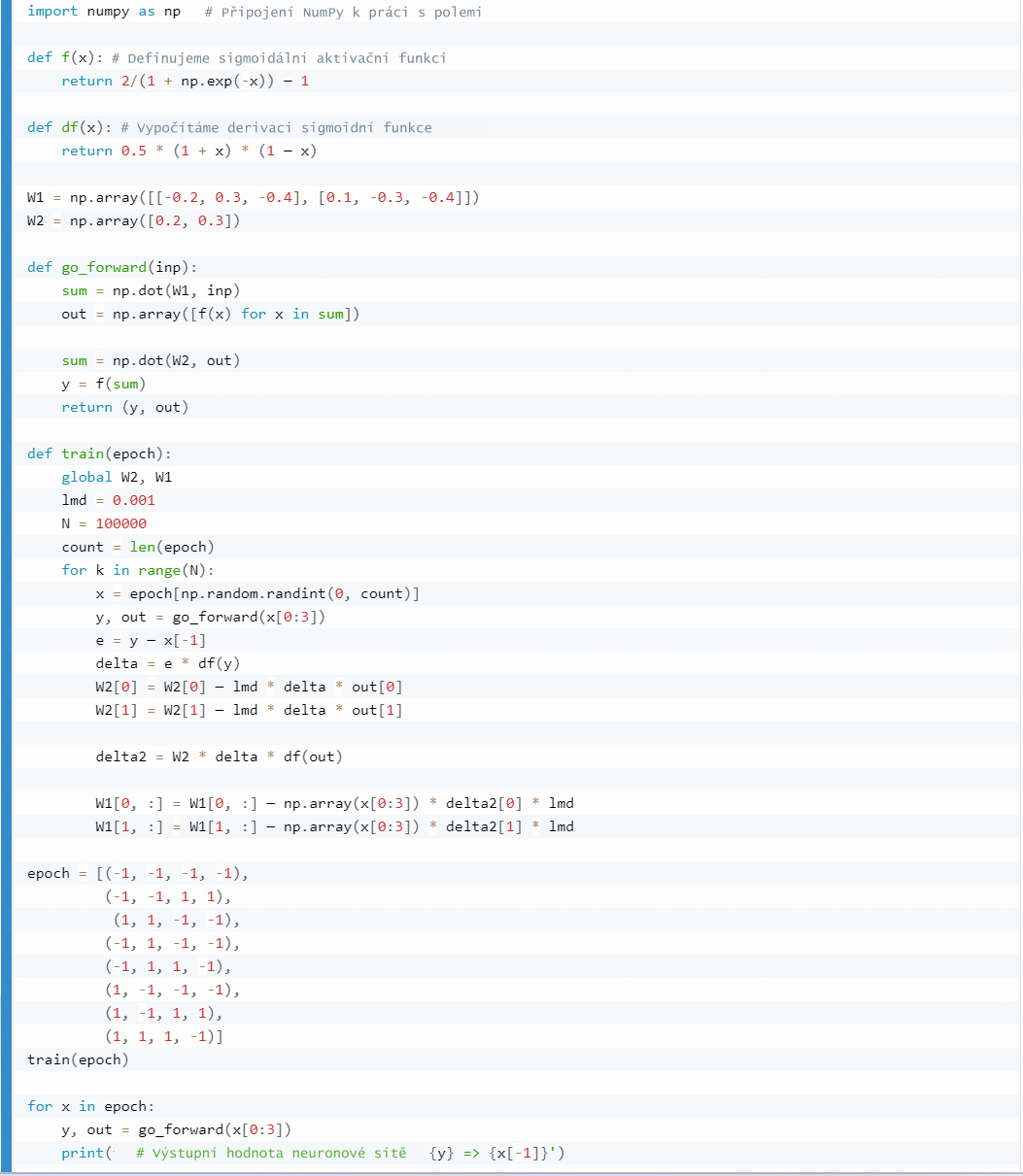
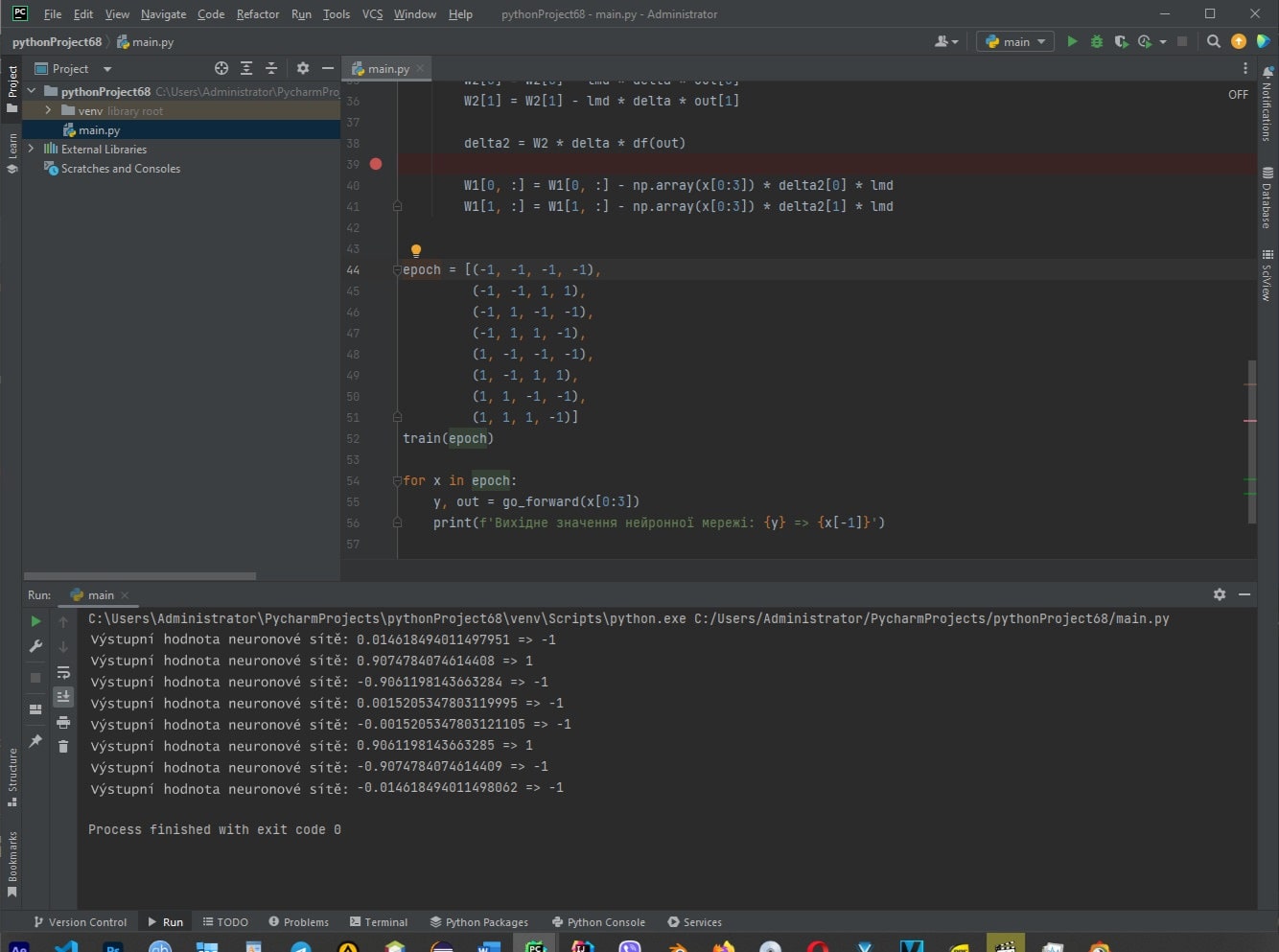
Výsledek kódu

Závěr

Pokud máš stále potíže s pochopením gradientního sestupu, představ si rokli se spoustou kamenů, do které se kutálí míč. Kutálí se ke dnu po náhodné trajektorii a naráží na náhodné prohlubně a římsy. Proces trénování neuronové sítě si lze představit jako sestup této kuličky: čím déle padá, tím více se blíží minimu funkce.

Kulička, která se kutálí dolů, představuje parametry modelu neuronové sítě a její cesta dolů roklí odpovídá změně parametrů modelu pomocí gradientního sestupu.

Při sestupu se kulička na své cestě setkává s různými překážkami, které mohou být podobné lokálním minimům chybové funkce. Čím déle se kulička kutálí dolů, tím blíže se může dostat k nejhlubší části rokle, což odpovídá minimalizaci chybové funkce a dosažení optimálních hodnot parametrů modelu neuronové sítě.

Nejtěžší je zvolit tréninkový krok tak, aby se gradientní sestup nerozcházel a netrval příliš dlouho. Někdy se může stát, že gradienty předávané vahám sítě budou velmi malé nebo velmi velké, což ztěžuje aktualizaci vah a zpomaluje konvergenci algoritmu. V takových situacích se používají různé metody normalizace a inicializace vah a výběr aktivačních funkcí.

Autor: Bondarenko Serhii